中国科学院高能物理研究所、日本理化学研究所与北京大学组成的研究团队,提出了一种无需引入辅助比特即可计算关联函数的量子算法。相关研究成果以“Computing n-time correlation functions without ancilla qubits”为题,于2025年12月3日正式发表于《物理评论快报》(Phys. Rev. Lett. 135, 230602 (2025))。
n 点时间关联函数在连接量子系统的理论预言与实验观测方面具有核心作用,被广泛应用于凝聚态物理、高能物理和计算化学等多个研究方向。由于计算此类关联函数需要模拟量子系统在多时刻的演化,对经典计算机而言极具挑战性,因此也被视为在现有量子硬件上展示实用量子优势的潜在途径。传统量子算法测量n点关联函数通常依赖辅助比特来控制整个系统(Phys. Rev. Lett. 113, 020505 (2014)),这一要求对量子比特连接度有限的数字量子计算机,以及缺乏受控门操作的模拟量子平台都构成了显著限制。
本项工作提出了一套仅利用目标系统自身幺正演化的计算 n 点关联函数的新方法,消除了对辅助量子比特和受控门操作的依赖,显著降低了硬件连接度的要求,使 n 点关联函数的测量在真实量子平台上更加可行。其核心思想是将关联函数拆解为对易子与反对易子的组合,并分别对应到量子线路上算符的实时与虚时演化。研究团队利用至多 12 个超导量子比特,演示了对施温格模型强子谱以及横场伊辛模型非时序关联函数(OTOC)的计算。通过引入基于经典信号处理(结合信号滤波与关联分析)的误差缓解方案,研究团队成功提取到了相对误差为0.18%的强子质量,并利用OTOC展示了横场伊辛模型可积性的相关特征。
本项研究为探索复杂量子多体系统的动力学行为提供了一条切实可行的途径,即使在受限硬件条件下仍能高效准确地测量n点关联函数。该方法的低硬件需求也有望促进其在量子化学、量子材料模拟等基础和应用领域的进一步发展,对量子混沌、量子热化及大规模量子模拟研究具有重要推动作用。
该工作的第一作者为日本理化学研究所数理创造研究中心的王啸洋,通信作者为中国科学院高能物理研究所的蔡肖夏和北京大学前沿计算研究中心的袁骁。本研究得到了国家自然科学基金委员会、中国科学院高能物理研究所引进人才项目等相关项目的资助。
论文链接:https://journals.aps.org/prl/abstract/10.1103/z126-zdqj
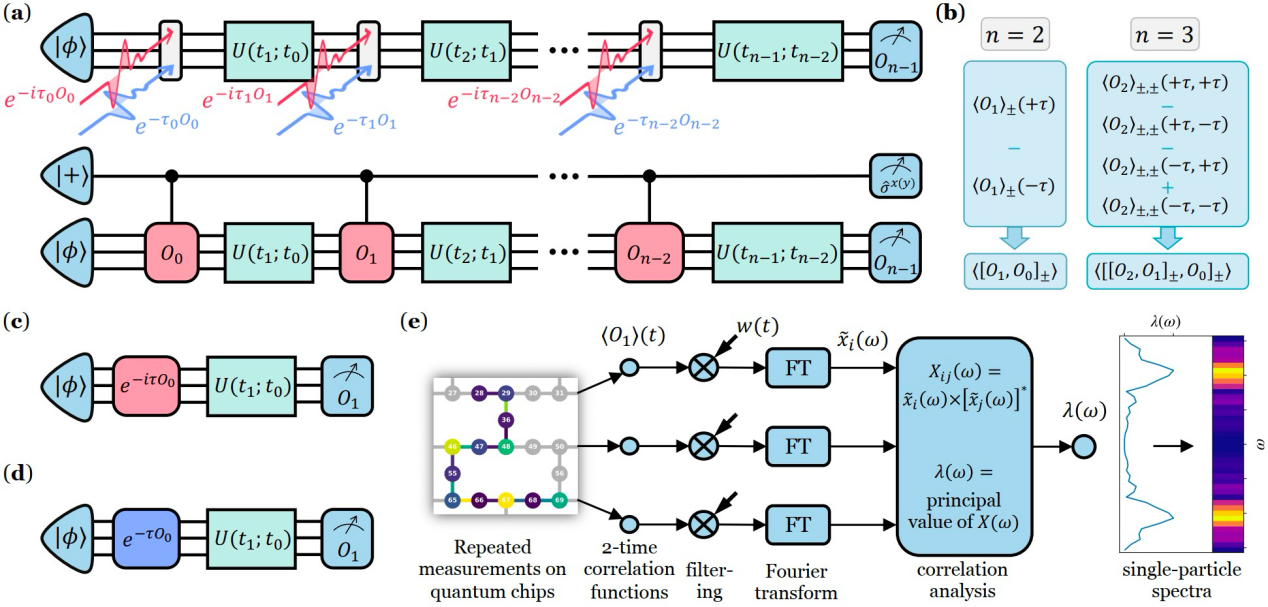
算法的核心计算思路与流程:1. n点关联函数可分解为算符对易子与反对易子的线性组合。 2. 对易(反对易)子对应算符实时(虚时)演化的期望值导数;期望值由线路(a)测量。 3. 利用参数移位规则(Parameter-Shift Rule),实现期望值导数的精确计算;如图(b)所示。
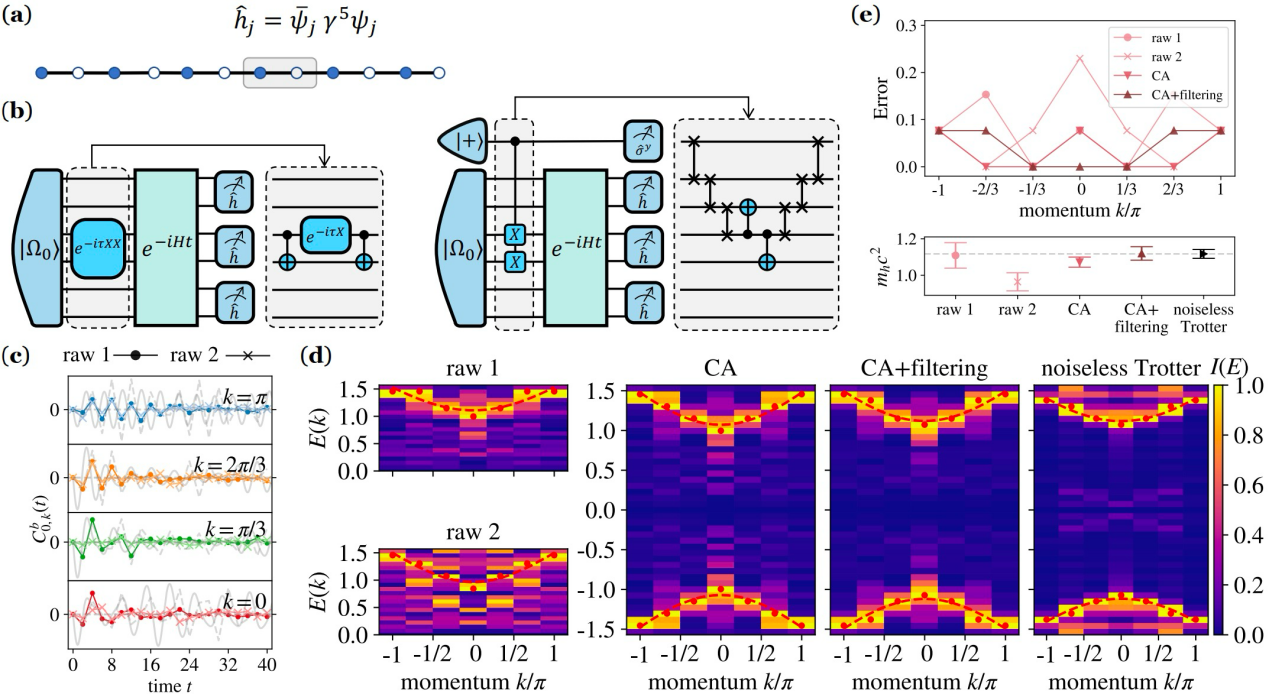
施温格模型强子谱的实验计算结果,结合信号滤波与关联分析可提取到相对误差为0.18%的强子质量。新方案可极大降低线路拓扑结构的限制以及所需两比特门数量。
附件下载: